前言

多數 AI 開發專案都不可避免地遇到這樣的問題：機器學習模型進入到部署階段並且開始服務後，隨著時間推移，資料分布出現飄移的情況，導致模型準確度隨著時間下降，最終使得專案的預期目標無法達成。

舉一個錯誤偵測模型應用於製造業的例子：假設有個模型的輸入為產品的生產歷程，輸出為該產品是否有瑕疵，即使這個模型在驗證集和測試集上都已經取得了符合要求的表現，等到模型開始上線運作之後，仍有許多因素可能使得資料的分布改變，例如機台隨著時間的損耗或者製造的原物料品質浮動等等，而這些因素都有可能讓模型表現漸漸不如預期，導致這個錯誤偵測模型的應用難以長久落地。

這種情況一般稱作為概念飄移 (concept drift)，概念飄移描述資料的分布隨著時間變化，使得根據過去資料歸納出來的規則以及訓練出來的模型，難以適用在新搜集的資料，並且降低模型預測的準確率或是導致錯誤的決策。

概念飄移對於機器學習模型的開發和部署帶來了非常大的挑戰。從模型開發的角度來說，假設訓練資料就已經存在概念飄移的情況，如何設計能夠適應資料分布不斷改變的模型，讓模型在訓練資料上的表現可以免於概念飄移的負面影響，甚至讓模型上線後也能自動地適應不同的資料分布，至今仍是活躍的研究議題。

而從模型部署的角度來說，模型開發者必須在模型上線後持續地監控模型表現，然而如何判斷模型表現確實受到概念飄移的污染，以及如何進行模型重訓練以校正模型的準確度，這些議題在實務上也有許多不同的討論和做法。

要解決以上的種種問題，必須要掌握概念飄移的幾個基本來源和類型。本文將從概念飄移的來源以及類型兩個角度，說明概念飄移呈現的不同形式。

概念飄移的來源

本文以下使用二元分類作為例子進行說明，令 $X$ 為特徵的隨機變數，且 $y$ 為二元標籤的隨機變數，目標是要給定一組 $X$ 得到預測的 $y$。假設在 $t$ 時間下觀察到了特徵 $X$ 與標籤 $y$ 的聯合分布 $P_t(X,y)$，根據貝氏定理可以進一步得到 $P_t(X,y)=P_t(X)P_t(y|X)$。

你現在也許已經開始混亂了，原本好好地要討論概念飄移，怎麼突然冒出了聯合分布 $P_t(X,y)$，又突然要把聯合分布進行拆解？這邊可以回過頭想一想，概念飄移要討論是「資料隨著時間變化」這件事情，而在二元分類的情境下，所擁有的資料正是 $X$ 與 $y$，這兩者的共同分布（也就是聯合分布）就是 $P(X,y)$。為了探討這個聯合分布在時間上的變化，又多了一個在 $t$ 時間下的假設，才會是最一開始提到的 $P_t(X,y)$。

至於為何要將 $P_t(X,y)$ 進行拆解？是因為單從 $P_t(X,y)$ 這個式子本身會如何隨著時間變化難以看出端倪，拆解成 $P_t(X)$ 和 $P_t(y|X)$ 兩個部分後，才能進一步研究 $P_t(X,y)$ 變化背後的成因。$P_t(X)$ 可以理解為在 $t$ 時間下特徵資料 $X$ 的分布，而 $P_t(y|X)$ 可以理解為在 $t$ 時間下，給定了一組特徵之後二元標籤的分布。由於透過 $P_t(y|X)$ 可以觀察出不同的特徵對應到的二元標籤，故 $P_t(y|X)$ 也可以視為 $t$ 時間下二元標籤的決策界線 (decision boundary)。

因此根據以上的拆解，當概念飄移發生，也就是 $P_t(X,y)\neq P_{t+1}(X,y)$ 時，飄移可能的來源有以下三種。

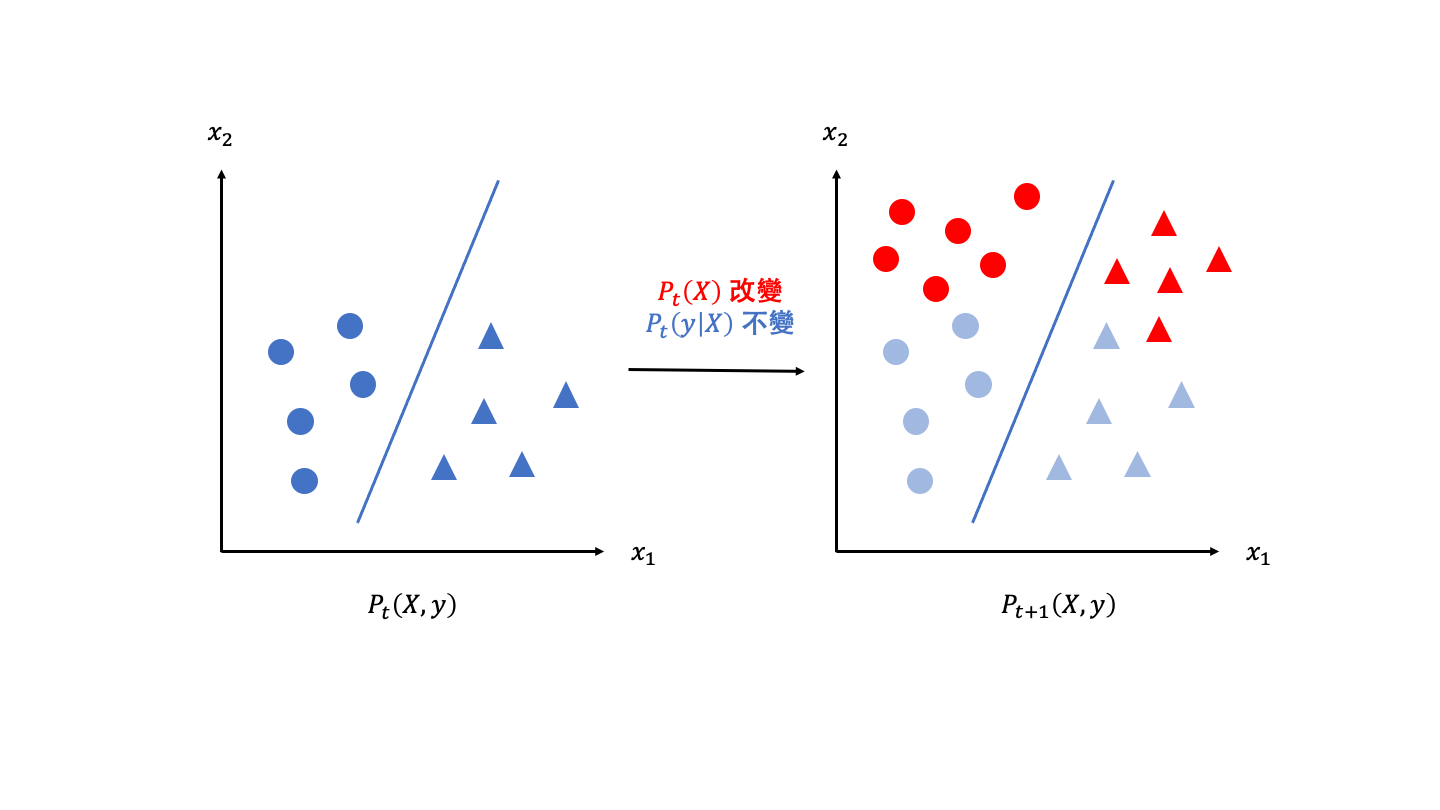
  1. $P_t(X)\neq P_{t+1}(X)$，代表在決策界線沒有改變的前提之下，特徵資料分布發生改變，這種飄移的特性在於只有模型輸入的分布改變，輸入和輸出間的關係則保持不變，因此對於模型表現的損害有限。又因決策界線沒有發生改變，這種來源的飄移又被稱作虛擬飄移 (virtual drift)，其他名稱包括資料飄移 (data drift) 以及共變量飄移 (covariate drift)。

下圖為虛擬飄移的示意圖，藍色的圓形和三角形代表 $t$ 時間之下的資料分布（特徵與二元標籤），藍色的線代表 $t$ 時間之下的決策界線，而紅色的點則代表 $t+1$ 時間下產生變化之後的結果。從圖中可以看到，只要決策界線維持不變，即便特徵的分布出現偏移，模型仍能維持相同的表現水準。

concept_drift_01_01.png

  1. $P_t(y|X)\neq P_{t+1}(y|X)$，代表特徵資料分布本身沒有改變，而是決策界線發生變動，這種飄移由於輸入和輸出間的關係發生了改變，在 $t$ 時間訓練的模型無法適用在 $t+1$ 時間的資料，導致模型準確度的下降。

下圖為第二類飄移來源的示意圖，同樣地藍色的點與線為 $t$ 時間之下的資料分布以及決策界線，紅色的點與線則為在 $t+1$ 時間下變化的結果。從圖中可以發現雖然特徵分布本身沒有改變，也就是資料仍散布在相同的區域，但是由於決策界線發生改變（紅色的線），使得在 $t$ 時間下部分的圓形的區域到了 $t+1$ 時間後變為三角形，反之亦然，此時若使用舊有的模型所學習到的決策界線（藍色的線）進行分類，就會出現準確率下降的情況。

concept_drift_01_02.png

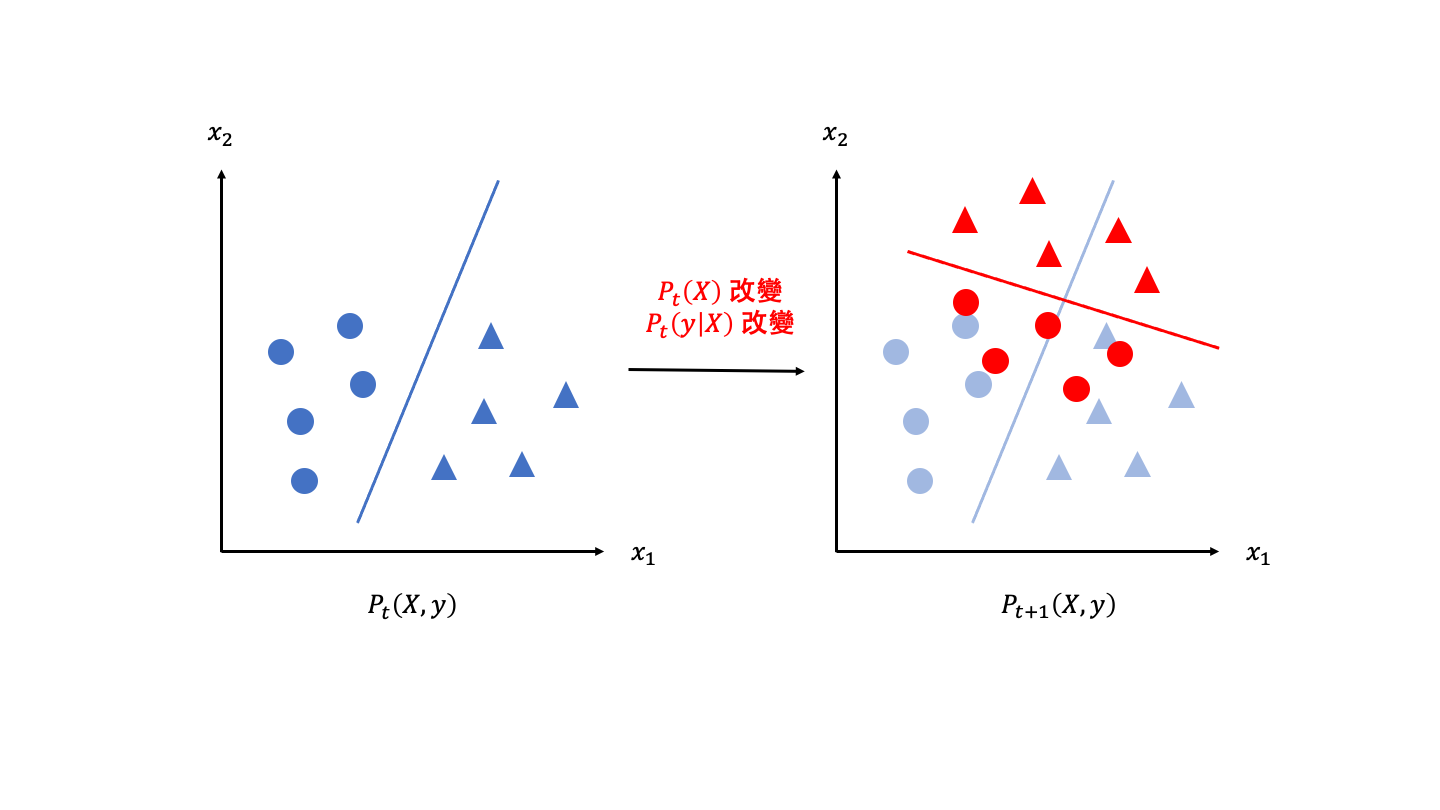
  1. $P_t(X)\neq P_{t+1}(X)$ 並且 $P_t(y|X)\neq P_{t+1}(y|X)$，代表特徵資料分布和決策界線都發生改變，這類飄移融合了前面兩種飄移的來源，輸入資料的分布以及輸入和輸出間的關係一起改變。一般在沒有特定指涉的情況下，概念飄移所指的是第三種情境。

下圖為概念飄移的示意圖，可以看到綜合了前面兩種來源的飄移形式，在圖上呈現的同樣也是舊有的模型無法對於新的時間點的資料作出準確的推論。

concept_drift_01_03.png

雖然此處將資料改變的來源比較細緻地分成三個部分討論，不過在一般的討論中，最常見的分類是資料飄移以及概念飄移兩種（也就是先前所列的第一種與第三種），以凸顯並非所有的資料分布改變都會影響模型輸入和輸出的關係。

此外，在釐清飄移的不同來源之後，就能理解不同的測量概念飄移的演算法，所能夠捕捉到的飄移來源，這部分之後會再進一步分享！

概念飄移的類型

討論完了概念飄移的來源之後，接下來說明概念飄移可能呈現的類型，一般而言可以分成四種，分別為突發性飄移 (sudden drift)、增強性飄移 (incremental drift)、漸進性飄移 (gradual drift) 以及再發性飄移 (reocurring drift)。

突發性飄移為資料分布發生快速且強烈的變化，增強性飄移描述資料改變的過程經歷某些中間狀態，最後轉變為不同的資料分布。漸進性飄移強調資料改變的過程會在兩種不同的狀態之間震盪，最終穩定趨向不同的資料分布。再發性飄移說明資料不斷地在已發生過的狀態之間重複出現。不同概念飄移的類型借用論文 A Survey on Concept Drift Adaptation 的圖，如下所示。

concept_drift_01_04.png

在不同的應用情境之下經常有不同的飄移類型，而具體所屬的類型需要透過資料分析或者領域知識 (domain knowledge) 的支持才能夠決定，在確定飄移的形式之後，相關的飄移偵測或者學習演算法的設計，都會圍繞在這個預先給定的飄移類型之下發展。換句話說，飄移類型和演算法之間有一定程度的相依，沒有一種應對概念飄移的演算法可以完美處理不同類型的飄移，舉例來說，假設已經知道在某個應用情境之中的概念飄移類型為漸進性飄移，那些專門用於突發性飄移的演算法在這個情境下就只能達到有限的效果。

結語

本文在概念上說明了概念飄移的來源以及類型，雖然在分析的過程中沒有涉及太多的數學或演算法，然而未來討論到如何測量概念飄移以及應對概念飄移的方法時，模型和演算法的設計都會和飄移的來源以及類型有非常密切的相關。

舉個例子來說，假設在一個資料會發生突發性飄移的情境中，使用定期模型重訓練的策略來應對資料分布的改變，就有可能出現模型表現已經大幅下降，卻仍然因為尚未到重訓練的時間點，導致這樣脫離常軌的模型無法被修正而繼續服務。如果能夠對飄移的類型有所掌握，並在模型的設計或者部署的機制上做出相對應的調整，例如設定一個給定的閾值，在模型的表現偏差到了一定的程度時，便立即重啟模型重訓練的機制，如此就能避免過時模型持續服務的情況。

瞭解概念飄移的來源、類型以及這些觀念的重要性之後，在下一篇文章將接著討論，如何判斷概念飄移是否存在，或者換句話說，如何測量概念飄移？

參考資料：

  1. Gama, J., Žliobaitė, I., Bifet, A., Pechenizkiy, M., & Bouchachia, A. (2014). A survey on concept drift adaptation. ACM Computing Surveys (CSUR), 46(4), 1-37.

  2. Lu, J., Liu, A., Dong, F., Gu, F., Gama, J., & Zhang, G. (2018). Learning under concept drift: A review. IEEE Transactions on Knowledge and Data Engineering, 31(12), 2346-2363.

如果你對這篇文章的內容有任何的想法或者指教，都歡迎來信和我討論~

下集待續：資料的滄海桑田 (II) - 概念飄移的測量